En matemàtiques, la funció poligamma d'ordre m, denotada  o
o  , és una funció meromorfa sobre els nombres complexos ℂ definida com la (m + 1)-èsima derivada logarítmica de la funció gamma:
, és una funció meromorfa sobre els nombres complexos ℂ definida com la (m + 1)-èsima derivada logarítmica de la funció gamma:

Així,
 és la funció digamma
és la funció digamma  , i
, i  és la funció gamma. Són holomorfes en ℂ \ −ℕ0. En tots els enters no-positius, aquestes funcions poligamma tenen un pol d'ordre m + 1.
és la funció gamma. Són holomorfes en ℂ \ −ℕ0. En tots els enters no-positius, aquestes funcions poligamma tenen un pol d'ordre m + 1. . De vegades
. De vegades  (o
(o  ) s'anomena funció trigamma.
) s'anomena funció trigamma.
Definició per una integral
Quan m > 0 i Re z > 0, la funció poligamma és igual a

Això expressa la funció poligamma com la transformada de Laplace  . Es deriva del teorema de Bernstein sobre les funcions monòtones que, per a m > 0 i x real i no-negatiu,
. Es deriva del teorema de Bernstein sobre les funcions monòtones que, per a m > 0 i x real i no-negatiu,  és una funció completament monòtona.
és una funció completament monòtona.
Fent m = 0 a la fórmula anterior no dona una representació integral de la funció digamma. La funció digamma té una representació integral, a causa de Gauss, que és similar al m = 0 del cas anterior, però amb el terme addicional  .
.
-
Gràfica la funció del poligamma al llarg de l'eix real amb m = 0 (taronja), m = 1 (groc), m = 2 (verd), m = 3 (vermell) i m = 4 (blau)
Representació en el pla complex
La representació del logaritme de la funció gamma i dels primers ordres de la funció poligamma en el pla complex és:
-

-

-

-

-

-

Relació de recurrència
Satisfa la relació de recurrència

cosa que (considerada per un argument sencer positiu) condueix a la presentació de la suma de reciprocs de les potències dels nombres naturals:

i

per a tot n ∈ ℕ.
Igual que la funció log-gamma, les funcions poligamma es poden generalitzar des del domini ℕ exclusivament a nombres reals positius només per la seva relació de recurrència i per un valor de funció donat ψ(m)(1), excepte en el cas m = 0 on la condició addicional d'estricta monotonia en ℝ+ encara es necessària. Aquesta és una conseqüència trivial del teorema de Bohr-Mollerup per a la funció gamma en què també s'exigeix la convexitat estrictament logarítmica ℝ+. El cas m = 0 s'ha de tractar d'una altra manera perquè ψ(0) no és normalitzable a l'infinit (la suma dels recíprocs no convergeix).
Relació de reflexió

on Pm és alternativament un polinomi de senar o parell de grau  amb coeficients enters i coeficient principal (−1)m⌈2m − 1⌉. Aquest obeeix l'equació de la recursió
amb coeficients enters i coeficient principal (−1)m⌈2m − 1⌉. Aquest obeeix l'equació de la recursió

Teorema de multiplicació
El teorema de multiplicació dona

i

per a la funció digamma.
Representació en sèries
La funció poligamma té la representació en sèries

que es mantè m > 0, i qualsevol z complex no és igual a un nombre enter negatiu. Aquesta representació es pot escriure de manera més compacta en termes de la funció zeta de Hurwitz

Alternativament, es pot entendre que la zeta de Hurwitz generalitza la funció poligamma a un ordre arbitrari, no-enter.
Es pot permetre una sèrie més per a les funcions poligamma. Tal com va donar Oskar Schlömilch,

Aquest és el resultat del teorema de factorització de Weierstrass. Per tant, la funció gamma ara es pot definir com:

Ara, el logaritme natural de la funció gamma és fàcilment representable:

Finalment, arribem a una representació amb sumatoris per a la funció poligamma:

On δn0 és la delta de Kronecker.
També el transcendent de Lerch

es pot denotar en termes de funció poligamma

Sèries de Taylor
La sèrie de Taylor a z = 1 és

i

que convergeix per a  . Aquí, ζ és la funció zeta de Riemann. Aquesta sèrie es deriva fàcilment de la corresponent sèrie de Taylor per a la funció zeta de Hurwitz. Aquesta sèrie es pot utilitzar per obtenir un nombre de les sèries racionals zeta.
. Aquí, ζ és la funció zeta de Riemann. Aquesta sèrie es deriva fàcilment de la corresponent sèrie de Taylor per a la funció zeta de Hurwitz. Aquesta sèrie es pot utilitzar per obtenir un nombre de les sèries racionals zeta.
Sèrie asimptòtica
Aquestes sèries no convergents es poden utilitzar per obtenir ràpidament un valor aproximat amb una certa precisió numèrica per a arguments grans:

i

on hem triat B1 = 1/2, és a dir, els nombres de Bernoulli del segon tipus.
Desigualtats
La cotangent hiperbòlica satisfà la desigualtat

i això implica que la funció

sigui no-negativa per a tot  i
i  . Es dedueix que la transformació de Laplace d'aquesta funció és completament monòtona. Mitjançant la representació integral anterior, arribem a la conclusió que
. Es dedueix que la transformació de Laplace d'aquesta funció és completament monòtona. Mitjançant la representació integral anterior, arribem a la conclusió que

és completament monòtona. La desigualtat de convexitat  implica que
implica que

és no-negativa per a tot  i
i  , de manera que un argument similar de transformació de Laplace produeix la completa monotonia de
, de manera que un argument similar de transformació de Laplace produeix la completa monotonia de

Per tant, per a tot m ≥ 1 i x > 0,

Alguns valors particulars
S'ha demostrat que:

on  és la constant d'Euler-Mascheroni. Aquesta sèrie, per a
és la constant d'Euler-Mascheroni. Aquesta sèrie, per a  enters positius, es redueix a una suma finita:
enters positius, es redueix a una suma finita:

Derivant membre a membre respecte a  obtenim
obtenim

que per a  divergeix, mentre per
divergeix, mentre per  es converteix en una sèrie harmònica generalitzada d'ordre 2
es converteix en una sèrie harmònica generalitzada d'ordre 2
![{\displaystyle \left[{\frac {d}{dz}}{\frac {\Gamma '{(z)}}{\Gamma {(z)}}}\right]_{z=1}=\psi _{1}(1)=\sum _{k=0}^{\infty }{\frac {1}{(1+k)^{2}}}=\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}=\zeta (2)={\frac {\pi ^{2}}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e57dca2da2a9efe4702fc7723086557b630290a)
Referències
- Abramowitz, Milton; Stegun, Irene A. «Section 6.4». A: Handbook of Mathematical Functions (en anglès). Nova York: Dover Publications, 1964, p. 260. ISBN 978-0-486-61272-0.
Vegeu també

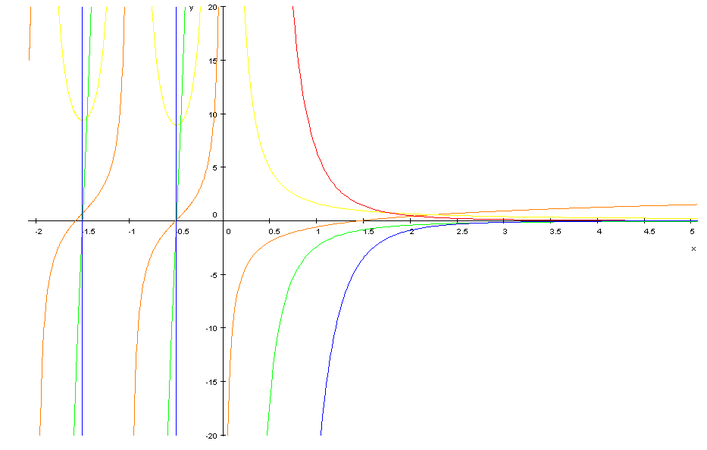 Gràfica la funció del poligamma al llarg de l'eix real amb m = 0 (taronja), m = 1 (groc), m = 2 (verd), m = 3 (vermell) i m = 4 (blau)
Gràfica la funció del poligamma al llarg de l'eix real amb m = 0 (taronja), m = 1 (groc), m = 2 (verd), m = 3 (vermell) i m = 4 (blau)













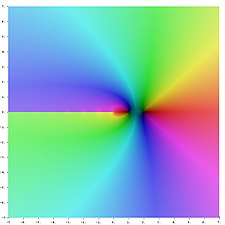



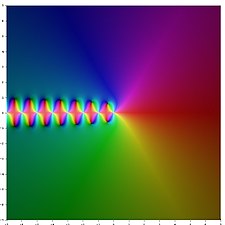





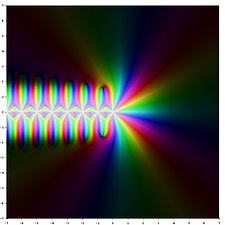







































![{\displaystyle \left[{\frac {d}{dz}}{\frac {\Gamma '{(z)}}{\Gamma {(z)}}}\right]_{z=1}=\psi _{1}(1)=\sum _{k=0}^{\infty }{\frac {1}{(1+k)^{2}}}=\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}=\zeta (2)={\frac {\pi ^{2}}{6}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e57dca2da2a9efe4702fc7723086557b630290a)
