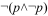Arithmétique de Heyting

L'arithmétique de Heyting est une axiomatisation de l'arithmétique dans le cadre de la logique intutionniste. Elle a été développée à l'origine par Arend Heyting.

Définition

L'arithmétique de Heyting^[1] est une théorie du premier ordre égalitaire sur la signature ${\displaystyle \{0,S,+,\times ,\leq \}}$, dont les axiomes sont les axiomes de Peano, close par déduction logique pour le calcul des prédicats intuitionniste^[2], tandis que l'arithmétique de Peano est close par déduction logique pour le calcul des prédicats classique. Certains auteurs^[3],[4] étendent le langage de l'arithmétique avec des symboles de fonctions pour chaque fonction primitive récursive.

En particulier, dans l'arithmétique de Heyting, si ${\displaystyle P}$ est une formule quelconque, ${\displaystyle P\lor \neg P}$ n'est pas nécessairement démontrable.

On note ${\displaystyle \mathbf {HA} \vdash P}$ pour dire que l'arithmétique de Heyting démontre la proposition ${\displaystyle P}$, et ${\displaystyle \mathbf {PA} \vdash P}$ pour dire que l'arithmétique de Peano démontre ${\displaystyle P}$.

Propriétés logiques

Certains principes logiques valides en logique classique ne sont pas valides en logique intuitionniste. En effet, de manière générale, ${\displaystyle P\lor \neg P}$, ou ${\displaystyle \neg \neg P\implies P}$ ou ${\displaystyle \exists nP\iff \neg \forall n\neg P}$ sont démontrables en logique classique mais pas en logique intuitionniste. Néanmoins, pour certaines formules en particulier, ces principes peuvent être vrais.

Décidabilité et tiers exclu

Une formule ${\displaystyle P}$ est dite décidable si ${\displaystyle \mathbf {HA} \vdash P\lor \neg P}$. Cette définition correspond à la notion de décidabilité algorithmique du problème « ${\displaystyle P}$ est-elle logiquement décidable par ${\displaystyle \mathbf {HA} }$ ? ». En effet, dans la correspondance de Curry-Howard, une démonstration de ${\displaystyle \mathbf {HA} \vdash P\lor \neg P}$ correspond à un programme qui produit soit une démonstration de ${\displaystyle P}$, soit une démonstration de ${\displaystyle \neg P}$. Il ne faut pas confondre cette notion avec celle de décidabilité logique par ${\displaystyle \mathbf {HA} }$ elle-même, qui caractérise les propositions ${\displaystyle P}$ telles que ${\displaystyle \mathbf {HA} \vdash P}$ ou ${\displaystyle \mathbf {HA} \vdash \neg P}$ indépendamment de la décidabilité algorithmique ou non de cette question.

En logique classique, toutes les formules sont décidables : c'est le tiers exclu. L'arithmétique de Heyting démontre que l'égalité est décidable : ${\displaystyle \mathbf {HA} \vdash \forall x\forall y(x=y\lor x\neq y)}$, ainsi que l'ordre : ${\displaystyle \mathbf {HA} \vdash \forall x\forall y(x\leq y\lor x\not \leq y)}$ (sachant que comme en logique classique, en logique intuitionniste on a équivalence entre une formule et sa clôture universelle (en), ces assertions en sont bien de décidabilité suivant la définition donnée ci-dessus, les quantifications universelles n’y étant qu’accessoires à équivalence près). De plus l'arithmétique de Heyting vérifie le principe de trichotomie : ${\displaystyle \mathbf {HA} \vdash \forall x\forall y(x<y\lor x=y\lor x>y)}$. On peut montrer que si ${\displaystyle P}$ est une formule ${\displaystyle \Delta _{0}^{0}}$, ${\displaystyle P}$ est décidable.

Élimination de la double négation

En logique classique, on a ${\displaystyle P\iff \neg \neg P}$, tandis qu'en logique intuitionniste, seule la version plus faible ${\displaystyle P\implies \neg \neg P}$ est vraie en général. Néanmoins, certaines classes de formules ${\displaystyle P}$ présentent aussi la propriété ${\displaystyle \mathbf {HA} \vdash \neg \neg P\implies P}$. C'est en particulier le cas pour les formules décidables et pour les formules de Harrop^[5].

On peut également formuler une réciproque faible de l'élimination de la double négation pour les formules ${\displaystyle \Sigma _{1}^{0}}$. Le principe de Markov énonce que si ${\displaystyle \neg \neg \exists nP}$ est démontrable, alors ${\displaystyle \exists nP}$ aussi. C'est un résultat plus faible que la démontrabilité de ${\displaystyle \neg \neg \exists nP\implies \exists nP}$. Ce principe est admissible^[3] pour un certain nombre de classes de formules ${\displaystyle P}$ :

• pour les formules ${\displaystyle \Delta _{0}^{0}}$. On le note ${\displaystyle \mathrm {MP} _{\mathrm {QF} }}$.

• pour le prédicat T de Kleene (en). On le note ${\displaystyle \mathrm {MP} _{0}}$.
• pour les prédicats primitifs récursifs. On le note ${\displaystyle \mathrm {MP} _{\mathrm {PR} }}$.
• pour les formules décidables, c'est-à-dire pour les formules ${\displaystyle P}$ telles que ${\displaystyle \mathbf {HA} \vdash P\lor \neg P}$. On le note ${\displaystyle \mathrm {MP} _{\mathrm {Dec} }}$.

Liens avec l'arithmétique de Peano

Les règles de déduction de la logique intuitionniste étant valides en logique classique, tout théorème de l'arithmétique de Heyting est aussi un théorème de l'arithmétique de Peano : si ${\displaystyle \mathbf {HA} \vdash P}$ alors ${\displaystyle \mathbf {PA} \vdash P}$. On peut formuler plusieurs réciproques partielles de ce théorème.

Traduction par double négation et équicohérence

Article détaillé : non-non traduction (en)

Kurt Gödel et Gerhard Gentzen ont proposé la traduction^[3] suivante ${\displaystyle P^{-}}$ d'une formule ${\displaystyle P}$ :

• ${\displaystyle \bot ^{-}=\bot }$ .
• ${\displaystyle P^{-}=\neg \neg P}$ si ${\displaystyle P}$ est atomique.
• ${\displaystyle (P\to Q)^{-}=P^{-}\to Q^{-}}$.
• ${\displaystyle (P\land Q)^{-}=P^{-}\land Q^{-}}$.
• ${\displaystyle (P\lor Q)^{-}=\neg \neg (P^{-}\lor Q^{-})}$.
• ${\displaystyle (\forall nP)^{-}=\forall nP^{-}}$.
• ${\displaystyle (\exists nP)^{-}=\neg \neg \exists nP^{-}}$.

Cette traduction possède les propriétés suivantes :

• Si ${\displaystyle \mathbf {PA} \vdash P}$ alors ${\displaystyle \mathbf {HA} \vdash P^{-}}$. En particulier si ${\displaystyle P}$ ne contient ni disjonction ni quantificateur existentiel, ${\displaystyle \mathbf {PA} \vdash P\iff \mathbf {HA} \vdash P}$.
• ${\displaystyle \mathbf {PA} \vdash P\iff P^{-}}$.
• ${\displaystyle \mathbf {HA} \vdash \neg \neg P^{-}\implies P^{-}}$.
• ${\displaystyle \mathbf {HA} \vdash (P^{-})^{-}\iff P^{-}}$.

On peut aussi montrer que si ${\displaystyle P}$ est une formule ${\displaystyle \Delta _{0}^{0}}$, ${\displaystyle \mathbf {HA} \vdash P\iff P^{-}}$.

Cette traduction a notamment permis à Gödel^[6] de montrer l'équicohérence de ${\displaystyle \mathbf {PA} }$ et ${\displaystyle \mathbf {HA} }$ : si ${\displaystyle \mathbf {PA} \vdash \bot }$ alors ${\displaystyle \mathbf {HA} \vdash \bot ^{-}}$, or ${\displaystyle \bot ^{-}=\bot }$ donc ${\displaystyle \mathbf {HA} \vdash \bot }$.

Conservativité

En utilisant à la fois la traduction par double-négation, le principe de Markov pour les formules ${\displaystyle \Delta _{0}^{0}}$ et le fait qu'une formule ${\displaystyle \Delta _{0}^{0}}$ est équivalente à sa traduction par double-négation, on peut montrer que si ${\displaystyle P}$ est une formule ${\displaystyle \Pi _{2}^{0}}$, alors ${\displaystyle \mathbf {PA} \vdash P\iff \mathbf {HA} \vdash P}$^[3].

Ce résultat implique notamment que si l'arithmétique de Peano démontre qu'une machine de Turing fixée s'arrête quelque soit son entrée, c'est-à-dire si elle représente une fonction récursive totale, alors l'arithmétique de Heyting le démontre également^[7].

Propositions indépendantes

Une proposition ${\displaystyle P}$ est dite indépendante d'une théorie si cette théorie ne démontre ni ${\displaystyle P}$, ni sa négation ${\displaystyle \neg P}$. Toute proposition indépendante de ${\displaystyle \mathbf {PA} }$ est aussi indépendante de ${\displaystyle \mathbf {HA} }$, mais certaines propositions démontrées par ${\displaystyle \mathbf {PA} }$ sont indépendantes de ${\displaystyle \mathbf {HA} }$. Étant donné qu'une théorie incohérente démontre toutes les propositions, toute cette section supposera la cohérence de ${\displaystyle \mathbf {HA} }$.

Principe de disjonction

L'arithmétique de Heyting vérifie le principe de disjonction ${\displaystyle \mathrm {DP} }$^[4]. Si ${\displaystyle P}$ et ${\displaystyle Q}$ sont des propositions closes (sans variables libres) :

Ce principe est vrai pour la logique intuitionniste propositionnel et est qualifié comme étant une bonne propriété pour les théories intuitionnistes. On en déduit que pour tout formule ${\displaystyle P}$, ${\displaystyle P}$ est indépendante de ${\displaystyle \mathbf {HA} }$ si et seulement si ${\displaystyle P\lor \neg P}$ l'est. Une telle proposition ${\displaystyle P}$ fournit ainsi un exemple de propositions pour laquelle le tiers exclu est invalide.

De plus, si ${\displaystyle P}$ est indépendante de ${\displaystyle \mathbf {PA} }$, alors ${\displaystyle \neg P}$ est aussi indépendante de ${\displaystyle \mathbf {PA} }$ donc de ${\displaystyle \mathbf {HA} }$, y compris si ${\displaystyle P}$ et ${\displaystyle \neg \neg P}$ ne sont pas équivalentes dans ${\displaystyle \mathbf {HA} }$. Ceci permet également de conclure que le principe du tiers exclu faible est faux dans ${\displaystyle \mathbf {HA} }$. Ce principe énonce que pour toute proposition ${\displaystyle P}$, ${\displaystyle \mathbf {HA} \vdash \neg P\lor \neg \neg P}$. En revanche, si ${\displaystyle P}$ n'est indépendante que de ${\displaystyle \mathbf {HA} }$, alors ${\displaystyle \neg P}$ n'est pas nécessairement indépendante de ${\displaystyle \mathbf {HA} }$. Par exemple, si ${\displaystyle Q}$ est indépendante de ${\displaystyle \mathbf {HA} }$, ${\displaystyle P=Q\lor \neg Q}$ est indépendante de ${\displaystyle \mathbf {HA} }$ mais pas ${\displaystyle \neg P}$ puisque ${\displaystyle \mathbf {HA} \vdash \neg \neg P}$.

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Heyting arithmetic » (voir la liste des auteurs).

Voir aussi

Bibliographie

• (en) Arend Heyting, Intuitionism: An Introduction, Amsterdam, North-Holland Publishing Company, 1971, 3^e éd. (1^re éd. 1956) (ISBN 978-0-7204-2239-9). 
• (en) Applied Proof Theory: Proof Interpretations and their Use in Mathematics (DOI 10.1007/978-3-540-77533-1, lire en ligne).
• (en) Morten Heine Sørensen et Pawel Urzyczyn, Lectures on the Curry-Howard Isomorphism, Elsevier, coll. « Studies in Logic and the Foundations of Mathematics » (n^o 149), 2006, 442 p. (ISBN 9780080478920, lire en ligne). 

Articles connexes

• Arithmétique

• Axiomes de Peano
• Logique intutionniste

• Portail des mathématiques
• Portail de la logique