2の自然対数

2の自然対数（にのしぜんたいすう）は、自然対数関数 log x の x = 2 での値であり、log 2 と表記する。2の常用対数との混同を避けるため ln 2 あるいは底を明記して loge 2 とも書かれる。log 2 は正の実数であり、その値は

log 2 = 0.69314 71805 59945 30941 72321…

である。この数は無理数であるので数字の循環しない無限小数である。さらに超越数であるため、代数方程式の解にはならない。連分数表記では

log 2 = [0; 1, 2, 3, 1, 6, 3, 1, 1, 2, 1, 1, 1, 1, 3, 10, …]

となる。また、この数は、核反応や化学反応において物質濃度の半減期を求める際に現れる数である。

定義

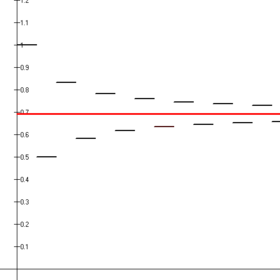1 − 1/2 + 1/3 − 1/4 + ... という級数の部分和（黒線）が log 2（赤線）に収束する様子

ネイピア数 e を底とした実数 x を変数とする対数関数 log x が x = 2 のときにとる値が log 2 である。対数関数は指数関数の逆関数であるので、

ez = 2

を満たすただ一つの実数の z が log 2 である。

対数関数のテイラー展開は

log ⁡ ( 1 + x ) = ∑ n = 1 ∞ ( − 1 ) n + 1 n x n ( | x | < 1 ) {\displaystyle \log(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}\quad (|x|<1)}

である。これに形式的に x = 1 を代入すると

log ⁡ 2 = ∑ n = 1 ∞ ( − 1 ) n + 1 n = 1 − 1 2 + 1 3 − 1 4 + ⋯ {\displaystyle \log 2=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\cdots }

となるが、この級数は実際に log 2 に収束することが知られている（→交項級数、アーベルの連続性定理）。

数学的性質

ディリクレのイータ関数（英語版）は

η ( s ) = ∑ n = 1 ∞ ( − 1 ) n + 1 n s {\displaystyle \eta (s)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{s}}}}

と定義されるので、上記のテイラー展開から、

η(1) = log 2

である。また、log 2 は以下のような級数でも求められる。

  • log ⁡ 2 = ∑ n = 1 ∞ 1 n ⋅ 2 n {\displaystyle \log 2=\sum _{n=1}^{\infty }{\frac {1}{n\cdot 2^{n}}}}
  • log ⁡ 2 = ∑ n = 0 ∞ ( − 1 ) n ( 1 3 n + 1 − 1 3 n + 2 + 1 3 n + 3 ) {\displaystyle \log 2=\sum _{n=0}^{\infty }(-1)^{n}\left({\frac {1}{3n+1}}-{\frac {1}{3n+2}}+{\frac {1}{3n+3}}\right)}
  • log ⁡ 2 = 1 2 ∑ n = 0 ∞ 1 ( − 4 ) n ( 2 4 n + 1 − 1 4 n + 3 − 1 4 n + 4 ) {\displaystyle \log 2={\frac {1}{2}}\sum _{n=0}^{\infty }{\frac {1}{(-4)^{n}}}\left({\frac {2}{4n+1}}-{\frac {1}{4n+3}}-{\frac {1}{4n+4}}\right)}
  • log ⁡ 2 = 1 3 ∑ n = 0 ∞ 1 ( − 27 ) n ( 3 6 n + 1 − 2 6 n + 3 − 1 6 n + 4 ) {\displaystyle \log 2={\frac {1}{3}}\sum _{n=0}^{\infty }{\frac {1}{(-27)^{n}}}\left({\frac {3}{6n+1}}-{\frac {2}{6n+3}}-{\frac {1}{6n+4}}\right)}

さらに、

∑ n = 1 ∞ ( − 1 ) n + 1 n {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}}

の第 N 項までの部分和と log 2 との差は

∑ n = 1 N ( − 1 ) n + 1 n − log ⁡ 2 = ( − 1 ) N ( 1 2 N + ∑ n = 0 ∞ ( − 1 ) n T n 4 N N 2 n ) {\displaystyle \sum _{n=1}^{N}{\frac {(-1)^{n+1}}{n}}-\log 2=(-1)^{N}\left({\frac {1}{2N}}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}T_{n}}{4^{N}N^{2n}}}\right)}

と表される。ここで、Tn は n 番目のタンジェント数である。

積分では

∫ 1 2 d x x = log ⁡ 2 {\displaystyle \int _{1}^{2}{\frac {dx}{x}}=\log 2}

であるから、双曲線 y = 1/x と直線 x = 1, x = 2 および y = 0 （x 軸）とに囲まれた図形の面積は log 2 である。

リンデマンの定理より log 2 は超越数であり、したがって無理数である。

log 2 が正規数かどうかは分かっていない。

その他の性質

反応速度

原子核反応や化学反応の速度は、反応物質の濃度に比例する場合が多い。この法則をもとに濃度の半減期を求めると、以下のように log 2 が現れる。

まず濃度を C, 反応速度定数を k とおくと、C を時間 t で微分したものがこの場合の速度なので、

−dC/dt = kC

となる。濃度は単調減少するので、速度の符号は負であることに注意。ここで、

を与えて定積分すると、

∫ C 0 C 0 / 2 d C C = ∫ 0 τ − k d t {\displaystyle \int _{C_{0}}^{C_{0}/2}{\frac {dC}{C}}=\int _{0}^{\tau }-kdt}
log ⁡ C 0 / 2 C 0 = − k τ {\displaystyle \log {\frac {C_{0}/2}{C_{0}}}=-k\tau }

となり、

log 2 = kτ

となる。すなわち、上記の微分方程式で表されるあらゆる反応において、log 2 は反応速度定数と半減期の積になっている。

72の法則

複利計算における「倍増年」（元利合計が2倍になる年数）の近似計算にも log 2 が現れる。

元金を X (> 0)、年利率を r (> 0) とし、n 年後に元利合計が2倍になるとすれば、

X (1 + r)n = 2X

となる。この両辺の自然対数をとると

n log(1 + r) = log 2
n = log 2/log(1 + r)

ここで、r ≪ 1、すなわち r が 1 に比べて十分に小さい場合には、log(1 + r) ≒ r と近似できるので、

n ≒ (log 2)/r ≒ 0.693/r

となる。

すなわち「倍増年」は、「0.693を年利で割った値」又は「69.3を年利（%表示）で割った値」で近似できる。実用上は、69.3を切りの良い70や約数の多い72で置き換えることが多い。たとえば、年利が3%ならば、72÷3 = 24 なので、約24年後に元利合計が倍増する。この法則は、72の法則と呼ばれ、15世紀のイタリアで知られていた。

関連項目

外部リンク