Pelengkap (teori set)

Jika ${\displaystyle A}$ ialah luas berwarna merah dalam gambar ini...

… maka pelengkap ${\displaystyle A}$ ialah segala sesuatu yang lain.

Dalam teori set, pelengkap set ${\displaystyle A}$, sering kali dilambangkan oleh ${\displaystyle A^{c}}$ (atau ${\displaystyle A'}$),^[1][2] adalah unsur yang bukan di ${\displaystyle A}$.^[3]

Ketika semua set dalam pertimbangan dianggap menjadi subset diberikan set ${\displaystyle U}$, pelengkap mutlak ${\displaystyle A}$ ialah set unsur di ${\displaystyle U}$, tetapi bukan di ${\displaystyle A}$.

Pelengkap relatif ${\displaystyle A}$ terhadap sebuah set ${\displaystyle B}$, juga disebut beza set ${\displaystyle B}$ dan ${\displaystyle A}$, ditulis ${\displaystyle B\setminus A}$, adalah set unsur-unsur di ${\displaystyle B}$ tapi bukan di ${\displaystyle A}$.^[1]

Pelengkap mutlak

Takrifan

Jika ${\displaystyle A}$ ialah sebuah set, maka pelengkap mutlak ${\displaystyle A}$) ialah set unsur-unsur yang bukan di ${\displaystyle A}$ (dalam sebuah set lebih besar yang secara implisit ditakrifkan). Dengan kata lain, misalkan ${\displaystyle U}$ menjadi sebuah set yang berisi semua unsur-unsur yang diperhatikan, jika tidak ada yang perlu untuk menyebutkan ${\displaystyle U}$, sama ade kerana telah ditentukan sebelumnya, atau dengan jelas dan unik, maka pelengkap mutlak ${\displaystyle A}$ ialah pelengkap relatif ${\displaystyle A}$ di ${\displaystyle U}$:^[4]

${\displaystyle A^{c}=U-A}$

Atau secara formal:

${\displaystyle A^{c}=\{x\in U\mid x\notin A\}}$.

Pelengkap mutlak ${\displaystyle A}$ biasanya dilambangkan oleh ${\displaystyle A^{c}}$.^[1] Notasi lainnya termasuk ${\displaystyle {\overline {A}}}$, ${\displaystyle A'}$,^[3] ${\displaystyle \complement _{U}A}$, dan ${\displaystyle \complement A}$.^[5]

Sebagai contoh, andaikan bahawa semesta ialah set nombor bulat. Jika ${\displaystyle A}$ ialah set nombor ganjil, maka pelengkap ${\displaystyle A}$ adalah set nombor genap. Jika ${\displaystyle B}$ ialah set gandaan 3, maka pelengkap ${\displaystyle B}$ ialah set bilangan kongruen dengan 1 atau 2 modulo 3 (atau, secara ringkasnya, nombor bulat bukan gandaan 3).

Sifat-sifat

Andaikan ${\displaystyle A}$ dan ${\displaystyle B}$ menjadi dua set dalam sebuah semesta ${\displaystyle U}$. Identiti berikut merangkumi sifat-sifat pelengkap mutlak yang penting:

Hukum de Morgan:^[6]

• ${\displaystyle \left(A\cup B\right)^{c}=A^{c}\cap B^{c}}$.
• ${\displaystyle \left(A\cap B\right)^{c}=A^{c}\cup B^{c}}$.

• ${\displaystyle A\cup A^{c}=U}$.
• ${\displaystyle A\cap A^{c}=\varnothing }$.
• ${\displaystyle \varnothing ^{c}=U}$.
• ${\displaystyle U^{c}=\varnothing }$.
• Jika ${\displaystyle A\subseteq B}$, maka ${\displaystyle B^{c}\subseteq A^{c}}$.

(ini diikuti daripada kesetaraan syarat dengan kontrapositifnya).

Hukum pelengkap involusi atau ganda:

• ${\displaystyle (A^{c})^{c}=A}$.

Hubungan antara pelengkap mutlak dan relatif:

• ${\displaystyle A\setminus B=A\cap B^{c}}$.
• ${\displaystyle (A\setminus B)^{c}=A^{c}\cup B=A^{c}\cup (B\cap A)}$.

Hubungan dengan sebuah beza set:

• ${\displaystyle A^{c}\setminus B^{c}=B\setminus A}$.

Dua hukum pelengkap pertama di atas menunjukkan bahawa jika ${\displaystyle A}$ adalah sebuah set bukan kosong, subset ${\displaystyle U}$, maka ${\displaystyle \{A,A^{c}\}}$ ialah pemetakan ${\displaystyle U}$.

Pelengkap relatif

Takrifan

Jika ${\displaystyle A}$ dan ${\displaystyle B}$ ialah set, maka pelengkap relatif ${\displaystyle A}$ dalam ${\displaystyle B}$,^[6] juga disebut beza set ${\displaystyle B}$ dan ${\displaystyle A}$,^[7] adalah set unsur-unsur di ${\displaystyle B}$ tapi bukan di ${\displaystyle A}$.

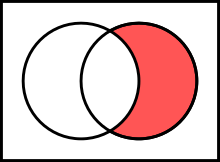
Pelengkap relatif ${\displaystyle A}$ di ${\displaystyle B}$ dilambangkan ${\displaystyle B\setminus A}$ berdasarkan piawai ISO 31-11. Kadangkala, ini ditulis sebagai ${\displaystyle B-A}$,^[1] tapi notasi ini bersifat samar kerana dalam beberapa konteks, ini dapat difahami sebagai set semua unsur ${\displaystyle b-a}$, di mana ${\displaystyle b}$ diambil dari ${\displaystyle B}$ dan ${\displaystyle a}$ diambil dari ${\displaystyle A}$.

Secara formal:

${\displaystyle B\setminus A=\{x\in B\mid x\notin A\}}$.

Contoh

• ${\displaystyle \{1,2,3\}\setminus \{2,3,4\}=\{1\}}$.
• ${\displaystyle \{2,3,4\}\setminus \{1,2,3\}=\{4\}}$.
• Jika ${\displaystyle \mathbb {R} }$ ialah set nombor nyata dan ${\displaystyle \mathbb {Q} }$ ialah set nombor nisbah, maka ${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$ ialah set nombor bukan nisbah.

Sifat-sifat

Andaikan ${\displaystyle A}$, ${\displaystyle B}$, dan ${\displaystyle C}$ menjadi tiga set. Identiti berikut merangkumi sifat-sifat penting pelengkap relatif:

• ${\displaystyle C\setminus (A\cap B)=(C\setminus A)\cup (C\setminus B)}$.
• ${\displaystyle C\setminus (A\cup B)=(C\setminus A)\cap (C\setminus B)}$.
• ${\displaystyle C\setminus (B\setminus A)=(C\cap A)\cup (C\setminus B)}$, dengan kes khusus penting ${\displaystyle C\setminus (C\setminus A)=(C\cap A)}$ menunjukkan bahawa persilangan dapat diungkapkan hanya menggunakan operasi pelengkap relatif.
• ${\displaystyle (B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A)}$.
• ${\displaystyle (B\setminus A)\cup C=(B\cup C)\setminus (A\setminus C)}$.
• ${\displaystyle A\setminus A=\emptyset }$.
• ${\displaystyle \emptyset \setminus A=\emptyset }$.
• ${\displaystyle A\setminus \emptyset =A}$.
• ${\displaystyle A\setminus U=\emptyset }$.

Hubungan pelengkap

Sebuah hubungan binari ${\displaystyle R}$ dapat ditakrifkan sebagai sebuah subset darab set ${\displaystyle X\times Y}$. Hubungan pelengkap ${\displaystyle {\bar {R}}}$ merupakan pelengkap set ${\displaystyle R}$ di ${\displaystyle X\times Y}$. Pelengkap relatif ${\displaystyle R}$ dapat ditulis

${\displaystyle {\bar {R}}\ =\ (X\times Y)\setminus R}$.

Di sini, ${\displaystyle R}$ sering kali dipandang sebagai sebuah matriks logik dengan baris mewakili unsur-unsur ${\displaystyle X}$, dan unsur-unsur lajur ${\displaystyle Y}$. Kebenaran mengenai ${\displaystyle aRb}$ berpadanan dengan 1 dalam baris ${\displaystyle a}$, lajur ${\displaystyle b}$. Menghasilkan hubungan pelenkap ke ${\displaystyle R}$, kemudian berpadanan dengan menukar semua 1 dan 0, dan 0 ke 1 bagi matriks logik dari pelengkap.

Bersama dengan pelengkap relatif dan hubungan songsang, hubungan pelengkap dan algebra set merupakan operasi-operasi asas dalam kalkulus relatif.

Notasi LaTeX

Dalam bahasa penyusunan huruf LaTeX, perintah \setminus ^[8]biasanya digunakan dalam mewakili sebuah simbol beza set yang serupa dengan sebuah simbol garis palang terbalik. Ketika diucapkan, perintah \setminus terlihat serupa dengan \backslash, kecuali bahawa ini memiliki sebuah ruang lebih sedikit di depan dan di belakang palang, sama dengan barisan LaTeX \mathbin{\backslash}. Sebuah varian \smallsetminus tersedia dalam pek amssymb.

Rujukan

Bibliografi

• Bourbaki, N. (1970). Théorie des ensembles (dalam bahasa Perancis). Paris: Hermann. ISBN 978-3-540-34034-8.
• Devlin, Keith J. (1979). Fundamentals of contemporary set theory. Universitext. Springer. ISBN 0-387-90441-7. Zbl 0407.04003.
• Halmos, Paul R. (1960). Naive set theory. The University Series in Undergraduate Mathematics. van Nostrand Company. Zbl 0087.04403.

Pautan luar

• Eric W. Weisstein, Complement di MathWorld.
• Eric W. Weisstein, Complement Set di MathWorld.Templat:Teori set