Função injectiva
Na matemática, uma função injectiva (ou injetora) é uma função que preserva a distinção: nunca aponta elementos distintos de seu domínio para o mesmo elemento de seu contradomínio. Em outras palavras, cada elemento do contradomínio da função é a imagem de no máximo um elemento de seu domínio. Ou seja, Uma função diz-se injectiva (ou injetora) se e somente se quaisquer que sejam e (pertencentes ao domínio da função), é diferente de implica que f() é diferente de f():
-
 Uma função injetiva, mas não sobrejetiva (injeção, mas é não uma bijeção)
Uma função injetiva, mas não sobrejetiva (injeção, mas é não uma bijeção) -
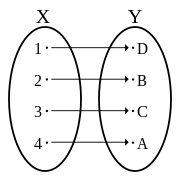 Uma função injetiva e sobrejetiva (bijeção)
Uma função injetiva e sobrejetiva (bijeção) -
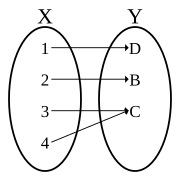 Uma função sobrejetiva, mas não injetiva (sobrejeção, não é uma bijeção)
Uma função sobrejetiva, mas não injetiva (sobrejeção, não é uma bijeção) -
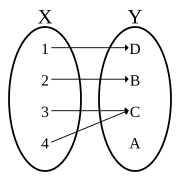 Uma função nem injetiva, nem sobrejetiva (também não é uma bijeção)
Uma função nem injetiva, nem sobrejetiva (também não é uma bijeção)
Graficamente, uma função é injectiva se e somente se nenhuma recta horizontal intersecta o seu gráfico em mais do que um ponto.
É importante notar que, neste tipo de função, o contradomínio tem uma cardinalidade sempre maior ou igual à do domínio. Além disso, pode haver mais elementos no contra-domínio que no conjunto imagem da função.
Ocasionalmente, uma função injetiva de a é denotada usando uma seta com uma "cauda separada" (U+21A3 ↣ RIGHTWARDS ARROW WITH TAIL).[1] O conjunto de funções injetivas de a pode ser denominado usando uma notação derivada daquela usada para decrescimento de potências fatoriais, uma vez que se e são conjuntos finitos com respectivamente e elementos, o número de injeções de a é
Um monomorfismo é uma generalização de uma função injetiva na teoria das categorias.
Definição
Seja uma função cujo domínio é um conjunto Diz-se que a função é injetiva desde que para todos e em sempre que então isto é, implica Equivalente, se então
Simbolicamente,
que é logicamente equivalente à contrapositiva,
Exemplos
- A função definida por não é injectiva, pois existe pelo menos um tal que por exemplo, para Isto é, o domínio da função admite que dois objectos distintos tenham a mesma imagem. Noutras palavras, existem dois valores diferentes que possam substituir a variável para que o valor da função seja igual a 4. Esses valores são 2 e -2.
- A função definida por é injectiva, pois implica que deve ser diferente de para Isto é, o domínio admite somente um valor para cada imagem. Como por exemplo, para que a função seja igual a 4, poderíamos substituir a variável somente pelo número 2.
- A função definida por é injectiva, pois implica que deve ser diferente de para Isto é, o domínio admite somente um valor para cada imagem. Como por exemplo, para que a função seja igual a 8, poderíamos substituir a variável somente pelo número 2, enquanto que para que a função seja igual a -8, poderíamos substituir a variável somente pelo número -2.
Aplicações lineares
- Uma transformação linear é dita injetora (ou injetiva) se, e somente se, o seu núcleo — ou ainda, — contiver apenas o vetor nulo e, pois, tiver dimensão zero — isto é,
A demonstração segue adiante:
→ Hipótese: T não é injetora → com para algum
Das propriedades da transformação linear:
→
Como u ≠ v ⇔ u - v ≠ 0, então:
→
O caso de T ser injetora é exclusivo e podemos afirmar que se
- Uma transformação linear também é dita injetiva se, e somente se, leva vetores L.I em vetores L.I. (LI = linearmente independentes)
Segue a demonstração:
→ Prova da ida:
Hipótese: A é injetiva
Tese: A leva vetores LI em vetores LI.
Se são linearmente independentes provaremos que são linearmente independentes.
Com efeito se
Usando a linearidade de A:
⇒
⇒
Então temos que pertence ao núcleo de e como é injetiva, ou seja,
, como são LI tem-se , ou seja são linearmente independentes.
← Prova da volta:
Hipótese: A leva vetores LI em vetores LI.
Tese: A é injetiva.
Sendo é LI então é portanto e é injetiva.
Segue-se desse teorema que se tem dimensão finita, assim por exemplo não existe transformação linear injetiva de em
Injeções podem ser desfeitas
Funções com inversas à esquerda são sempre injeções. Isto é, dado se houver uma função tal que, para cada
então é injetiva. Nesse caso, é chamada de retração de Por outro lado, é chamado de seção de
Inversamente, toda injeção com domínio não vazio tem uma inversa à esquerda, que pode ser definida fixando um elemento a no domínio de de modo que seja igual à pré-imagem única de sob se existir e caso contrário.[2]
A inversa à esquerda não é necessariamente um inverso de porque a composição na outra ordem, pode diferir da identidade em Em outras palavras, uma função injetora pode ser "invertida" por uma inversa à esquerda, mas é não necessariamente invertível, o que requer que a função seja bijetiva.
Injeções podem tornar-se invertíveis
Na verdade, para transformar uma função injetora em uma função bijetiva (portanto, invertível), basta substituir seu contradomínio pelo seu intervalo real Isto é, vamos tal que para todo em então g é bijetiva. De fato, pode ser fatorada como onde é a função de inclusão de em
Mais geralmente, as funções parciais injetivas são chamadas de bijeções parciais.
Outras propriedades
- Se e são ambas injetivas, então é injetiva.

- Se é injetiva, então é injetiva (mas não precisa ser).
- é injetiva se, e somente se, dadas quaisquer funções sempre que então Em outras palavras, funções injetivas são precisamente os monomorfismos na categoria Conjunto de conjuntos.
- Se é injetiva e é um subconjunto de então Assim, pode ser recuperado de sua imagem
- Se é injetiva e e são ambos subconjuntos de então
- Cada função pode ser decomposta como para uma injeção adequada e uma sobrejeção Esta decomposição é única até o isomorfismo, e pode ser considerada como a função de inclusão do intervalo de como um subconjunto do contradomínio de
- Se é uma função injetiva, então tem pelo menos tantos elementos quanto no sentido de números cardinais. Em particular, se, além disso, houver uma injeção de para então e terão o mesmo número cardinal. (Isso é conhecido como o teorema de Cantor-Bernstein-Schroeder.)
- Se tanto quanto são finitos com o mesmo número de elementos, então é injetiva se e somente se é sobrejetiva (nesse caso é bijetiva).
- Uma função injetiva que é um homomorfismo entre duas estruturas algébricas é uma incorporação.
- Ao contrário da sobrejetividade, que é uma relação entre o gráfico de uma função e seu contradomínio, a injetividade é uma propriedade do gráfico da função sozinha; isto é, se uma função é injetiva pode ser decidida considerando apenas o gráfico (e não o contradomínio) de
Provando que as funções são injetivas
Uma prova de que uma função é injetiva depende de como a função é apresentada e quais propriedades ela contém. Para funções que são dadas por alguma fórmula, há uma ideia básica. Usamos a contrapositiva da definição de injetividade, ou seja, se então [3]
Exemplo 1
Prova: Seja Suponha que Então, Portanto, segue da definição que é injetiva.
Exemplo 2
Existem vários outros métodos para provar que uma função é injetiva. Por exemplo, no cálculo se é uma função diferenciável definida em algum intervalo, então é suficiente mostrar que a derivada é sempre positiva ou sempre negativa nesse intervalo. Na álgebra linear, se é uma transformação linear, é suficiente mostrar que o núcleo de contém apenas o vetor zero. Se é uma função com domínio finito, basta olhar a lista de imagens de cada elemento de domínio e verificar se nenhuma imagem ocorre duas vezes na lista.
Ver também
| Outros projetos Wikimedia também contêm material sobre este tema: | |
 | Livros e manuais no Wikilivros |
|---|---|
- Wikilivros
Notas
- ↑ «Unicode» (PDF). Consultado em 11 de maio de 2013
- ↑ Ao contrário da afirmação correspondente de que toda função sobrejetiva tem um inverso à direita, isso não requer o axioma da escolha, já que a existência de a é implicada pela não-vacuidade do domínio. No entanto, esta afirmação pode falhar em matemática menos convencional, como a matemática construtiva. Na matemática construtiva, a inclusão {0,1} → 'R' do conjunto de dois elementos nos reais não pode ter inversão à esquerda, pois violaria indecomposição, dando uma retração da reta real para o conjunto {0,1}.
- ↑ Williams, Peter. «Proving Functions One-to-One». Cópia arquivada em 4 de junho de 2017
Referências
- Bartle, Robert G. (1976), The Elements of Real Analysis, ISBN 978-0-471-05464-1 2nd ed. , New York: John Wiley & Sons , p. 17 ff.
- Halmos, Paul R. (1974), Naive Set Theory, ISBN 978-0-387-90092-6, New York: Springer , p. 38 ff.
Ligações externas

- Aula sobre os tipos de funções
- Earliest Uses of Some of the Words of Mathematics: entry on Injection, Surjection and Bijection has the history of Injection and related terms.
- Khan Academy – Surjective (onto) and Injective (one-to-one) functions: Introduction to surjective and injective functions




































































































































