Komplemen (teori himpunan)

Jika ${\displaystyle A}$ adalah luas berwarna merah dalam gambar ini...

… maka komplemen ${\displaystyle A}$ adalah segala sesuatu yang lain.

Dalam teori himpunan, komplemen himpunan ${\displaystyle A}$, sering kali dilambangkan oleh ${\displaystyle A^{c}}$ (atau ${\displaystyle A'}$),^[1][2] adalah unsur yang bukan di ${\displaystyle A}$.^[3]

Ketika semua himpunan terhadap pertimbangan dianggap menjadi subhimpunan diberikan himpunan ${\displaystyle U}$, komplemen mutlak ${\displaystyle A}$ adalah himpunan unsur di ${\displaystyle U}$, tapi bukan di ${\displaystyle A}$.

Komplemen relatif ${\displaystyle A}$ terhadap sebuah himpunan ${\displaystyle B}$, juga disebut beda himpunan ${\displaystyle B}$ dan ${\displaystyle A}$, ditulis ${\displaystyle B\setminus A}$, adalah himpunan unsur-unsur di ${\displaystyle B}$ tapi bukan di ${\displaystyle A}$.^[1]

Komplemen mutlak

Definisi

Jika ${\displaystyle A}$ adalah sebuah himpunan, maka komplemen mutlak ${\displaystyle A}$) adalah himpunan unsur-unsur yang bukan di ${\displaystyle A}$ (dalam sebuah himpunan lebih besar yang secara implisit didefinisikan). Dengan kata lain, misalkan ${\displaystyle U}$ menjadi sebuah himpunan yang berisi semua unsur-unsur terhadap kajian, jika tidak ada yang perlu untuk menyebutkan ${\displaystyle U}$, baik karena ditentukan sebelumnya, atau dengan jelas dan unik, maka komplemen mutlak ${\displaystyle A}$ adalah komplemen relatif ${\displaystyle A}$ di ${\displaystyle U}$:^[4]

${\displaystyle A^{c}=U-A}$

Atau secara formal:

${\displaystyle A^{c}=\{x\in U\mid x\notin A\}}$.

Komplemen mutlak ${\displaystyle A}$ biasanya dilambangkan oleh ${\displaystyle A^{c}}$.^[1] Notasi lainnya termasuk ${\displaystyle {\overline {A}}}$, ${\displaystyle A'}$,^[3] ${\displaystyle \complement _{U}A}$, dan ${\displaystyle \complement A}$.^[5]

Contoh-contoh

• Asumsi bahwa semesta adalah himpunan bilangan bulat. Jika ${\displaystyle A}$ adalah himpunan bilangan ganjil, maka komplemen ${\displaystyle A}$ adalah himpunan bilangan genap. Jika ${\displaystyle B}$ adlaah himpunan kelipatan 3, maka komplemen ${\displaystyle B}$ adalah himpunan bilangan kongruen dengan 1 atau 2 modulo 3 (atau, dalam istilah yang lebih sederhana, bilangan bulatnya yang bukan merupakan kelipatan 3).
• Asumsi bahwa semesta adalah dek 52 kartu standar. Jika ${\displaystyle A}$ adalah kartu sekop, maka komplemen ${\displaystyle A}$ adalah gabungan dari kartu keriting, wajik, dan hati. Jika himpunan ${\displaystyle B}$ adalah gabungan dari kartu keriting dan wajik, maka komplemen ${\displaystyle B}$ adalah gabungan dari kartu hati dan sekop.

Sifat-sifat

Misalkan ${\displaystyle A}$ dan ${\displaystyle B}$ menjadi dua himpunan dalam sebuah semesta ${\displaystyle U}$. Identitas berikut menangkap sifat-sifat komplemen mutlak yang penting:

Hukum de Morgan:^[6]

• ${\displaystyle \left(A\cup B\right)^{c}=A^{c}\cap B^{c}}$.
• ${\displaystyle \left(A\cap B\right)^{c}=A^{c}\cup B^{c}}$.
• ${\displaystyle A\cup A^{c}=U}$.
• ${\displaystyle A\cap A^{c}=\varnothing }$.
• ${\displaystyle \varnothing ^{c}=U}$.
• ${\displaystyle U^{c}=\varnothing }$.
• Jika ${\displaystyle A\subseteq B}$, maka ${\displaystyle B^{c}\subseteq A^{c}}$.

(ini diikuti dari kesetaraan syarat dengan kontrapositifnya).

Hukum komplemen involusi atau ganda:

• ${\displaystyle (A^{c})^{c}=A}$.

Hubungan antara komplemen mutlak dan relatif:

• ${\displaystyle A\setminus B=A\cap B^{c}}$.
• ${\displaystyle (A\setminus B)^{c}=A^{c}\cup B=A^{c}\cup (B\cap A)}$.

Hubungan dengan sebuah beda himpunan:

• ${\displaystyle A^{c}\setminus B^{c}=B\setminus A}$.

Dua hukum komplemen pertama di atas menunjukkan bahwa jika ${\displaystyle A}$ adalah sebuah himpunan takkosong, subhimpunan wajar ${\displaystyle U}$, maka ${\displaystyle \{A,A^{c}\}}$ adalah penyekatan ${\displaystyle U}$.

Komplemen relatif

Definisi

Jika ${\displaystyle A}$ dan ${\displaystyle B}$ adalah himpunan, maka komplemen relatif ${\displaystyle A}$ dalam ${\displaystyle B}$,^[6] juga disebut beda himpunan ${\displaystyle B}$ dan ${\displaystyle A}$,^[7] adalah himpunan unsur-unsur di ${\displaystyle B}$ tapi bukan di ${\displaystyle A}$.

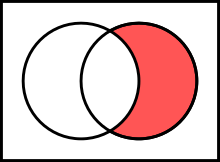
Komplemen relatif ${\displaystyle A}$ di ${\displaystyle B}$ dilambangkan ${\displaystyle B\setminus A}$ menurut standar ISO 31-11. Ini terkadang ditulis ${\displaystyle B-A}$,^[1] tapi notasi ini ambigu, karena dalam beberapa konteks, ini dapat diinterpretasikan sebagai himpunan semua unsur-unsur ${\displaystyle b-a}$, dimana ${\displaystyle b}$ diambil dari ${\displaystyle B}$ dan ${\displaystyle a}$ diambil dari ${\displaystyle A}$.

Secara formal:

${\displaystyle B\setminus A=\{x\in B\mid x\notin A\}}$.

Contoh-contoh

• ${\displaystyle \{1,2,3\}\setminus \{2,3,4\}=\{1\}}$.
• ${\displaystyle \{2,3,4\}\setminus \{1,2,3\}=\{4\}}$.
• Jika ${\displaystyle \mathbb {R} }$ adalah himpunan bilangan real dan ${\displaystyle \mathbb {Q} }$ adalah himpunan bilangan rasional, maka ${\displaystyle \mathbb {R} \setminus \mathbb {Q} }$ adalah himpunan bilangan irasional.

Sifat-sifat

Misalkan ${\displaystyle A}$, ${\displaystyle B}$, dan ${\displaystyle C}$ menjadi tiga himpunan. Identitas berikut menangkap sifat-sifat penting mengenai komplemen relatif:

• ${\displaystyle C\setminus (A\cap B)=(C\setminus A)\cup (C\setminus B)}$.
• ${\displaystyle C\setminus (A\cup B)=(C\setminus A)\cap (C\setminus B)}$.
• ${\displaystyle C\setminus (B\setminus A)=(C\cap A)\cup (C\setminus B)}$, dengan kasus khusus yang penting ${\displaystyle C\setminus (C\setminus A)=(C\cap A)}$ menunjukkan bahwa irisan dapat diungkapkan hanya menggunakan operasi komplemen relatif.
• ${\displaystyle (B\setminus A)\cap C=(B\cap C)\setminus A=B\cap (C\setminus A)}$.
• ${\displaystyle (B\setminus A)\cup C=(B\cup C)\setminus (A\setminus C)}$.
• ${\displaystyle A\setminus A=\emptyset }$.
• ${\displaystyle \emptyset \setminus A=\emptyset }$.
• ${\displaystyle A\setminus \emptyset =A}$.
• ${\displaystyle A\setminus U=\emptyset }$.

Relasi komplementer

Sebuah relasi biner ${\displaystyle R}$ didefinisikan sebagai sebuah subhimpunan darab himpunan ${\displaystyle X\times Y}$. Relasi komplementer ${\displaystyle {\bar {R}}}$ merupakan komplemen himpunan ${\displaystyle R}$ di ${\displaystyle X\times Y}$. Komplemen relasi ${\displaystyle R}$ dapat ditulis

${\displaystyle {\bar {R}}\ =\ (X\times Y)\setminus R}$.

Disini, ${\displaystyle R}$ sering kali dipandang sebagai sebuah matriks logis dengan baris mewakili unsur-unsur ${\displaystyle X}$, dan unsur-unsur kolom ${\displaystyle Y}$. Kebenaran mengenai ${\displaystyle aRb}$ berpadanan dengan 1 dalam baris ${\displaystyle a}$, kolom ${\displaystyle b}$. Menghasilkan relasi komplementer ke ${\displaystyle R}$, kemudian berpadanan dengan menukar semua 1 dan 0, dan 0 ke 1 untuk matriks logis dari komplemen.

Bersama dengan komplemen relasi dan relasi sebalik, relasi komplementer dan aljabar himpunan merupakan operasi-operasi elementer dari kalkulus relasi.

Notasi LaTeX

Dalam bahasa penyusunan huruf LaTeX, perintah \setminus^[8] biasanya digunakan untuk mengucapkan sebuah simbol beda himpunan, yang serupa dengan sebuah simbol garis miring terbalik. Ketika diucapkan, perintah \setminus terlihat identis dengan \backslash, kecuali bahwa ini memiliki sebuah ruang lebih sedikit di depan dan di belakang garis miring, sama dengan barisan LaTeX \mathbin{\backslash}. Sebuah varian \smallsetminus tersedia dalam pengepakan amssymb.

Dalam bahasa pemrograman

Beberapa bahasa pemrograman memiliki himpunan-himpunan di sekitar di bangun dalam struktur data. Seperti sebuah struktur data berperilaku sebagai sebuah himpunan hingga, yaitu, ini terdiri dari sebuah bilangan terhingga mengenai data yang bukan terurut secara khusus, dan dapat dengan demikian dianggap sebagai unsur-unsur himpunan. Dalam beberapa kasus, unsur-unsurnya tidak perlu beda, dan kode struktur data multihimpunan ketimbang himpunan. Bahasa pemrograman memiliki operator atau fungsi untuk menghitung komplemen dan beda himpunan.

Operator-operator ini dapat secara umum juga berlaku untuk struktur data yang bukan himpunan matematis sesungguhnya, seperti daftar terurut atau larik. Ini mengikuti bahwa beberapa bahasa pemrograman dapat memiliki sebuah fungsi disebut set_difference ,bahkan jika ini tidak memiliki suatu struktur data untuk himpunan.

Lihat pula

• Aljabar himpunan
• Irisan (teori himpunan)
• Daftar identitas himpunan dan relasi
• Teori himpunan naif
• Beda simetrik
• Gabungan (teori himpunan)

Catatan

1. ^ ^{a b c d} "Compendium of Mathematical Symbols". Math Vault (dalam bahasa Inggris). 2020-03-01. Diakses tanggal 2020-09-04. 
2. ^ "Complement and Set Difference". web.mnstate.edu. Diarsipkan dari versi asli tanggal 2021-01-23. Diakses tanggal 2020-09-04. 
3. ^ ^{a b} "Complement (set) Definition (Illustrated Mathematics Dictionary)". www.mathsisfun.com. Diakses tanggal 2020-09-04. 
4. ^ Himpunan yang komplemennya dianggap dengan demikian secara implisit ditentukan dalam sebuah komplemen mutlak, dan secara eksplisit ditentukan dalam sebuah komplemen relatif.
5. ^ Bourbaki 1970, hlm. E II.6.
6. ^ ^{a b} Halmos 1960, hlm. 17.
7. ^ Devlin 1979, hlm. 6.
8. ^ [1] Diarsipkan 2022-03-05 di Wayback Machine. The Comprehensive LaTeX Symbol List

Referensi

• Bourbaki, N. (1970). Théorie des ensembles (dalam bahasa Prancis). Paris: Hermann. ISBN 978-3-540-34034-8. 
• Devlin, Keith J. (1979). Fundamentals of contemporary set theory. Universitext. Springer. ISBN 0-387-90441-7. Zbl 0407.04003. 
• Halmos, Paul R. (1960). Naive set theory. The University Series in Undergraduate Mathematics. van Nostrand Company. Zbl 0087.04403. 

Pranala luar

• (Inggris) Weisstein, Eric W. "Complement". MathWorld. 
• (Inggris) Weisstein, Eric W. "Complement Set". MathWorld.