Nota: Para a tecla de computador, veja Delete.
Nota: Para Diodo emissor de luz, veja LED.
No cálculo vectorial , o del é um operador diferencial representado pelo símbolo nabla ( ∇ ) . {\displaystyle \left(\nabla \right).}
Derivada em função do espaço Seja um campo escalar diferenciável f {\displaystyle f} x → . {\displaystyle {\vec {x}}.}
∀ n ∈ N ∗ D n f = ∂ f ∂ x → n {\displaystyle \forall n\in \mathbb {N_{*}} \quad D_{n}f={\frac {\partial f}{\partial {\vec {x}}_{n}}}}
Em altas ordens A derivada em função do espaço em alta ordem é representada por uma multiplicação simbólica como no exemplo abaixo (de 2ª ordem):
∀ n , m ∈ N ∗ 2 D n D m f = D n ( D m f ) = ∂ ( ∂ f ∂ x → m ) ∂ x → n = ∂ 2 f ∂ x → n ∂ x → m {\displaystyle \forall n,m\in \mathbb {N_{*}} \!^{2}\quad D_{n}D_{m}f=D_{n}\left(D_{m}\,f\right)={\frac {\partial \left({\frac {\partial f}{\partial {\vec {x}}_{m}}}\right)}{\partial {\vec {x}}_{n}}}={\frac {\partial ^{2}f}{\partial {\vec {x}}_{n}\partial {\vec {x}}_{m}}}}
Essa operação é comutativa de acordo com o teorema de Clairaut-Schwarz, então, do exemplo acima pode-se afirmar que:
D n D m f = D m D n f {\displaystyle D_{n}D_{m}f=D_{m}D_{n}f}
Quando os índices são iguais podemos fazer uma exponenciação simbólica.
∀ k , n ∈ N ∗ 2 D n k f = D n D n ( … ) D n ⏟ k f = ∂ k f ∂ x → n k {\displaystyle \forall k,n\in \mathbb {N_{*}} \!^{2}\quad D_{n}^{k}f=\underbrace {D_{n}D_{n}\left(\ldots \right)D_{n}} _{k}f={\frac {\partial ^{k}f}{\partial {\vec {x}}\,_{n}^{k}}}}
Em outras coordenadas ortogonais Para todo sistema de coordenadas ortogonal q → {\displaystyle {\vec {q}}}
D n f = ∂ f q → n ∂ q → n {\displaystyle D_{n}f={\frac {\partial f}{{\vec {q}}_{n}\partial {\vec {q}}_{n}}}}
Operações Seja um campo escalar f {\displaystyle f} F → {\displaystyle {\vec {F}}} x → . {\displaystyle {\vec {x}}.}
Gradiente Visualização da interpretação de gradiente - o campo escalar domínio está em preto e a imagem, vectorial, em azul. Em cada ponto, o gradiente aponta para o vizinho que representar o maior incremento infinitesimal. O gradiente é um campo vectorial e seu domínio é um campo escalar.
∇ f = ∑ i D i f ⋅ e ^ i {\displaystyle \nabla f=\sum ^{i}D_{i}f\cdot {\hat {e}}_{i}}
Portanto o gradiente de f {\displaystyle f} x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle }
∇ f = ⟨ ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ⟩ {\displaystyle \nabla f=\left\langle {\frac {\partial f}{\partial x}},{\frac {\partial f}{\partial y}},{\frac {\partial f}{\partial z}}\right\rangle }
O processo de computação do gradiente é revertido pelo integral de linha de acordo com o teorema do gradiente.
Δ f = f Q − f P = ∫ γ P γ Q ∇ f ⋅ d γ → {\displaystyle \Delta f=f_{Q}-f_{P}=\int _{\gamma _{P}}^{\gamma _{Q}}\nabla f\cdot {\vec {d\gamma }}}
Identidades do gradiente ∇ ( f + g ) = ∇ f + ∇ g {\displaystyle \nabla (f+g)=\nabla f+\nabla g} ∇ ( f g ) = f ∇ g + g ∇ f {\displaystyle \nabla (fg)=f\nabla g+g\nabla f} Derivada direcional A derivada direcional é um escalar que representa a derivada dum campo escalar (no caso, f) ao longo de um vector (no caso abaixo, u → {\displaystyle {\vec {u}}} ∀ u → ∇ u → f = u → ⋅ ∇ f {\displaystyle \forall {\vec {u}}\quad \nabla \!_{\vec {u}}\,f={\vec {u}}\cdot \nabla f}
Em coordenadas cartesianas, u → ⋅ ∇ f = u x ∂ f ∂ x + u y ∂ f ∂ y + u z ∂ f ∂ z {\displaystyle {\vec {u}}\cdot \nabla f=u_{x}\;{\frac {\partial f}{\partial x}}+u_{y}\;{\frac {\partial f}{\partial y}}+u_{z}\;{\frac {\partial f}{\partial z}}}
Em coordenadas cilíndricas, u → ⋅ ∇ f = u r ∂ f ∂ r + u θ r ∂ f ∂ θ − u θ 2 r + u z ∂ f ∂ z {\displaystyle {\vec {u}}\cdot \nabla f=u_{r}\;{\frac {\partial f}{\partial r}}+{\frac {u_{\theta }}{r}}\;{\frac {\partial f}{\partial \theta }}-{\frac {u_{\theta }^{2}}{r}}+u_{z}\;{\frac {\partial f}{\partial z}}}
Divergência A divergência (ou divergente ) é um campo escalar igual ao traço (álgebra linear) da matriz jacobiana dum campo vectorial. ∇ ∙ F → = ∑ i D i F → i = Sp J x → F → {\displaystyle \nabla \bullet {\vec {F}}=\sum ^{i}D_{i}{\vec {F}}_{i}={\mbox{Sp}}\mathbf {J} _{\vec {x}}^{\vec {F}}}
Portanto a divergência de F → {\displaystyle {\vec {F}}} x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle } ∇ ∙ F → = ∂ F → x ∂ x + ∂ F → y ∂ y + ∂ F → z ∂ z {\displaystyle \nabla \bullet {\vec {F}}={\frac {\partial {\vec {F}}_{x}}{\partial x}}+{\frac {\partial {\vec {F}}_{y}}{\partial y}}+{\frac {\partial {\vec {F}}_{z}}{\partial z}}}
Denomina-se convergência o inverso aditivo da divergência.
Identidades da divergência ∇ ⋅ ( F → + G → ) = ∇ ⋅ F → + ∇ ⋅ G → {\displaystyle \nabla \cdot ({\overrightarrow {F}}+{\overrightarrow {G}})=\nabla \cdot {\overrightarrow {F}}+\nabla \cdot {\overrightarrow {G}}} Rotacional A rotacional (ou rotor ) é o determinante entre três bases padrões, três componentes do vector del e três componentes dum campo vectorial.
∇ × F → = ∑ i D i F → × e ^ i = ∑ i j k ε i j k ⋅ e ^ i ⋅ D j F → k {\displaystyle \nabla \times {\vec {F}}=\sum _{i}D_{i}{\vec {F}}\times {\hat {e}}_{i}=\sum _{ijk}\varepsilon _{ijk}\cdot {\hat {e}}_{i}\cdot D_{j}{\vec {F}}_{k}}
Pelo teorema de Laplace o rotor de F → {\displaystyle {\vec {F}}} x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle }
∇ × F → = ⟨ D y F → z − D z F → y , D z F → x − D x F → z , D x F → y − D y F → x ⟩ {\displaystyle {\begin{aligned}\nabla \times {\vec {F}}={\bigg \langle }&D_{y}{\vec {F}}_{z}-D_{z}{\vec {F}}_{y},\\&D_{z}{\vec {F}}_{x}-D_{x}{\vec {F}}_{z},\\&D_{x}{\vec {F}}_{y}-D_{y}{\vec {F}}_{x}{\bigg \rangle }\\\end{aligned}}}
Identidades do rotacional ∇ × ( F → + G → ) = ∇ × F → + ∇ × G → {\displaystyle \nabla \times ({\overrightarrow {F}}+{\overrightarrow {G}})=\nabla \times {\overrightarrow {F}}+\nabla \times {\overrightarrow {G}}} Operações combinadas Das nove possíveis simples combinações entre os operadores gradiente, divergente e rotor duas a duas, quatro são impossíveis, duas são triviais nulas (sempre resultam em zero) – restam três operadores dos quais um recebe um nome especial, que é o divergente do gradiente denominado laplaciano .
…gradiente de f {\displaystyle f} …divergente de F → {\displaystyle {\vec {F}}} …rotor de F → {\displaystyle {\vec {F}}} Gradiente do… (indefinido) Gradiente do divergente (indefinido) Divergente do… Laplaciano escalar (indefinido) (trivial nulo) Rotor do… (trivial nulo) (indefinido) Rotor do rotor
Todas essas três operações definidas e não-triviais são relacionadas pela seguinte identidade:
( ∑ i ∇ 2 F → i ) ⏟ l a p l a c i a n o v e c t o r i a l + ( ∇ × ∇ × F → ) ⏟ r o t o r d o r o t o r = ( ∇ ( ∇ ∙ F → ) ) ⏟ g r a d i e n t e d o d i v e r g e n t e {\displaystyle \underbrace {\left(\sum ^{i}\nabla ^{2}{\vec {F}}_{i}\right)} _{laplaciano\,vectorial}+\underbrace {\left(\nabla \times \nabla \times {\vec {F}}\right)} _{rotor\,do\,rotor}=\underbrace {\left(\nabla \left(\nabla \bullet {\vec {F}}\right)\right)} _{gradiente\,do\,divergente}}
Laplaciano O laplaciano escalar é o divergente do gradiente ou o traço (álgebra linear) da matriz hessiana dum campo escalar.
∇ 2 f = ∇ ∙ ∇ f = ∑ i D i 2 f = Sp H x → f {\displaystyle \nabla ^{2}f=\nabla \bullet \nabla f=\sum ^{i}D_{i}^{2}f={\mbox{Sp}}\mathbf {H} _{\vec {x}}^{f}}
Onde:
D i 2 f = D i ( D i f ) = ∂ 2 f ∂ x → i 2 {\displaystyle D_{i}^{2}f=D_{i}\left(D_{i}f\right)={\frac {\partial ^{2}f}{\partial {\vec {x}}_{i}^{2}}}}
O laplaciano de f {\displaystyle f} x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle } ∇ 2 f = ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 {\displaystyle \nabla ^{2}f={\frac {\partial ^{2}f}{\partial x^{2}}}+{\frac {\partial ^{2}f}{\partial y^{2}}}+{\frac {\partial ^{2}f}{\partial z^{2}}}}
Outras combinações ∇ ⋅ ( f F → ) = ( ∇ f ) ⋅ F → + f ( ∇ ⋅ F → ) {\displaystyle \nabla \cdot (f{\overrightarrow {F}})=(\nabla f)\cdot {\overrightarrow {F}}+f(\nabla \cdot {\overrightarrow {F}})} ∇ × ( f F → ) = ( ∇ f ) × F → + f ( ∇ × F → ) {\displaystyle \nabla \times (f{\overrightarrow {F}})=(\nabla f)\times {\overrightarrow {F}}+f(\nabla \times {\overrightarrow {F}})} ∇ ⋅ ( F → × G → ) = G → ⋅ ( ∇ × F → ) − F → ⋅ ( ∇ × G → ) {\displaystyle \nabla \cdot ({\overrightarrow {F}}\times {\overrightarrow {G}})={\overrightarrow {G}}\cdot (\nabla \times {\overrightarrow {F}})-{\overrightarrow {F}}\cdot (\nabla \times {\overrightarrow {G}})} ∇ ( F → ⋅ G → ) = ( G → ⋅ ∇ ) F → + ( F → ⋅ ∇ ) G → + G → × ( ∇ × F → ) + F → × ( ∇ × G → ) {\displaystyle \nabla ({\overrightarrow {F}}\cdot {\overrightarrow {G}})=({\overrightarrow {G}}\cdot \nabla ){\overrightarrow {F}}+({\overrightarrow {F}}\cdot \nabla ){\overrightarrow {G}}+{\overrightarrow {G}}\times (\nabla \times {\overrightarrow {F}})+{\overrightarrow {F}}\times (\nabla \times {\overrightarrow {G}})} ∇ × ( F → × G → ) = ( G → ⋅ ∇ ) F → − G → ( ∇ ⋅ F → ) − ( F → ⋅ ∇ ) G → + F → ( ∇ ⋅ G → ) {\displaystyle \nabla \times ({\overrightarrow {F}}\times {\overrightarrow {G}})=({\overrightarrow {G}}\cdot \nabla ){\overrightarrow {F}}-{\overrightarrow {G}}(\nabla \cdot {\overrightarrow {F}})-({\overrightarrow {F}}\cdot \nabla ){\overrightarrow {G}}+{\overrightarrow {F}}(\nabla \cdot {\overrightarrow {G}})} ∇ × ( ∇ × F → ) = ∇ ( ∇ ⋅ F → ) − ∇ 2 F → {\displaystyle \nabla \times (\nabla \times {\overrightarrow {F}})=\nabla (\nabla \cdot {\overrightarrow {F}})-\nabla ^{2}{\overrightarrow {F}}} f {\displaystyle f} F → {\displaystyle {\overrightarrow {F}}} ∇ × ( ∇ f ) = 0 → {\displaystyle \nabla \times (\nabla f)={\overrightarrow {0}}} f {\displaystyle f} F → {\displaystyle {\overrightarrow {F}}} ∇ ⋅ ( ∇ × F → ) = 0 {\displaystyle \nabla \cdot (\nabla \times {\overrightarrow {F}})=0} f {\displaystyle f} F → {\displaystyle {\overrightarrow {F}}} Laplaciano vectorial Cada componente do laplaciano vectorial representa o laplaciano do componente respectivo do campo vectorial argumento.
∇ 2 F → = ∑ i ∇ 2 F → i ⋅ e ^ i = ∑ i j D j 2 F → i ⋅ e ^ i = ∑ i Sp H x → F → i ⋅ e ^ i {\displaystyle \nabla ^{2}{\vec {F}}=\sum ^{i}\nabla ^{2}{\vec {F}}_{i}\cdot {\hat {e}}_{i}=\sum ^{ij}D_{j}^{2}{\vec {F}}_{i}\cdot {\hat {e}}_{i}=\sum ^{i}{\mbox{Sp}}\mathbf {H} _{\vec {x}}^{{\vec {F}}_{i}}\cdot {\hat {e}}_{i}}
Onde:
D j 2 F → i = D j ( D j F → i ) = ∂ 2 F → i ∂ x → j 2 {\displaystyle D_{j}^{2}{\vec {F}}_{i}=D_{j}\left(D_{j}{\vec {F}}_{i}\right)={\frac {\partial ^{2}{\vec {F}}_{i}}{\partial {\vec {x}}_{j}^{2}}}}
Portanto o laplaciano vectorial de F → {\displaystyle {\vec {F}}} x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle }
∇ 2 F → = ⟨ ∂ 2 F → x ∂ x 2 + ∂ 2 F → x ∂ y 2 + ∂ 2 F → x ∂ z 2 , ∂ 2 F → y ∂ x 2 + ∂ 2 F → y ∂ y 2 + ∂ 2 F → y ∂ z 2 , ∂ 2 F → z ∂ x 2 + ∂ 2 F → z ∂ y 2 + ∂ 2 F → z ∂ z 2 ⟩ {\displaystyle {\begin{aligned}\nabla ^{2}{\vec {F}}={\Bigg \langle }&{\frac {\partial ^{2}{\vec {F}}_{x}}{\partial x^{2}}}+{\frac {\partial ^{2}{\vec {F}}_{x}}{\partial y^{2}}}+{\frac {\partial ^{2}{\vec {F}}_{x}}{\partial z^{2}}},\\&{\frac {\partial ^{2}{\vec {F}}_{y}}{\partial x^{2}}}+{\frac {\partial ^{2}{\vec {F}}_{y}}{\partial y^{2}}}+{\frac {\partial ^{2}{\vec {F}}_{y}}{\partial z^{2}}},\\&{\frac {\partial ^{2}{\vec {F}}_{z}}{\partial x^{2}}}+{\frac {\partial ^{2}{\vec {F}}_{z}}{\partial y^{2}}}+{\frac {\partial ^{2}{\vec {F}}_{z}}{\partial z^{2}}}{\Bigg \rangle }\\\end{aligned}}}
Vector del Apesar de se tratar dum grave caso de abuso de notação, é muito comum se encontrar a seguinte definição de vector del :
∇ → = ∑ i q ^ i h i ⋅ ∂ ∂ x → i {\displaystyle {\vec {\nabla }}=\sum ^{i}{\frac {{\hat {q}}_{i}}{h_{i}}}\cdot {\frac {\partial }{\partial {\vec {x}}_{i}}}}
…onde h i {\displaystyle h_{i}} q ^ i . {\displaystyle {\hat {q}}_{i}.}
Em coordenadas cartesianas Em coordenadas cartesianas , em que h i = 1 {\displaystyle h_{i}=1}
∇ → = i ^ ∂ ∂ x + j ^ ∂ ∂ y + k ^ ∂ ∂ z . {\displaystyle {\overrightarrow {\nabla }}={\hat {i}}{\partial \over \partial x}+{\hat {j}}{\partial \over \partial y}+{\hat {k}}{\partial \over \partial z}.}
Em coordenadas cilíndricas Em coordenadas cilíndricas em que h ρ = h z = 1 , h φ = ρ , {\displaystyle h_{\rho }=h_{z}=1,\ h_{\varphi }=\rho ,}
∇ → = ρ ^ ∂ ∂ ρ + φ ^ ρ ∂ ∂ φ + z ^ ∂ ∂ z {\displaystyle {\overrightarrow {\nabla }}={\hat {\rho }}{\frac {\partial }{\partial \rho }}+{\frac {\hat {\varphi }}{\rho }}{\frac {\partial }{\partial \varphi }}+{\hat {z}}{\frac {\partial }{\partial z}}}
Em coordenadas esféricas Em coordenadas esféricas , em que h r = 1 , h θ = r , h φ = r s e n θ , {\displaystyle h_{r}=1,\ h_{\theta }=r,\ h_{\varphi }=r{\rm {sen}}\theta ,}
∇ → = r ^ ∂ ∂ r + θ ^ r ∂ ∂ θ + φ ^ r s e n θ ∂ ∂ φ {\displaystyle {\overrightarrow {\nabla }}={\hat {r}}{\frac {\partial }{\partial r}}+{\frac {\hat {\theta }}{r}}{\frac {\partial }{\partial \theta }}+{\frac {\hat {\varphi }}{r\,{\rm {sen}}\,\theta }}{\frac {\partial }{\partial \varphi }}}
Derivada direcional com o vector del Com o vector del, a derivada direcional pode ser redefinida como a combinação linear de u → {\displaystyle {\vec {u}}} ∇ → : {\displaystyle {\vec {\nabla }}:}
∇ → u → = ∑ i u → i ⋅ ∂ ∂ x → i = u → ⋅ ∇ → {\displaystyle {\vec {\nabla }}_{\vec {u}}=\sum ^{i}{\vec {u}}_{i}\cdot {\frac {\partial }{\partial {\vec {x}}_{i}}}={\vec {u}}\cdot {\vec {\nabla }}}
Em três dimensões no espaço carteseano x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle }
∇ → = ı ^ ⋅ ∂ ∂ x + ȷ ^ ⋅ ∂ ∂ y + k ^ ⋅ ∂ ∂ z = ⟨ ∂ ∂ x , ∂ ∂ y , ∂ ∂ z ⟩ {\displaystyle {\vec {\nabla }}={\hat {\imath }}\cdot {\frac {\partial }{\partial x}}+{\hat {\jmath }}\cdot {\frac {\partial }{\partial y}}+{\hat {k}}\cdot {\frac {\partial }{\partial z}}=\left\langle {\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}\right\rangle }
E:
∇ → u → = u → x ⋅ ∂ ∂ x + u → y ⋅ ∂ ∂ y + u → z ⋅ ∂ ∂ z {\displaystyle {\vec {\nabla }}_{\vec {u}}={\vec {u}}_{x}\cdot {\frac {\partial }{\partial x}}+{\vec {u}}_{y}\cdot {\frac {\partial }{\partial y}}+{\vec {u}}_{z}\cdot {\frac {\partial }{\partial z}}}
Divergência com o vector del A divergência passa a ser a combinação linear (não o produto escalar ! – veja abaixo) entre o vector del e o campo vectorial em questão:
∇ → ⋅ F → = ∑ i ∂ ∂ x → i ⋅ F → i {\displaystyle {\vec {\nabla }}\cdot {\vec {F}}=\sum ^{i}{\frac {\partial }{\partial {\vec {x}}_{i}}}\,\cdot \,{\vec {F}}_{i}}
Laplaciano com o vector del A combinação linear do vector del consigo mesmo forma o operador laplaciano:
∇ → 2 = ∇ → ⋅ ∇ → {\displaystyle {\vec {\nabla }}^{2}={\vec {\nabla }}\cdot {\vec {\nabla }}}
Em três dimensões no espaço carteseano x → = ⟨ x , y , z ⟩ {\displaystyle {\vec {x}}=\left\langle x,y,z\right\rangle }
∇ → 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 {\displaystyle {\vec {\nabla }}^{2}={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}}
Rotacional com o vector del Daí admitimos outro abuso de notação para definir rotacional:
∇ → × F → = det [ e ^ ∇ F → ] = det [ e ^ x e ^ y e ^ z ∂ ∂ x ∂ ∂ y ∂ ∂ z F → x F → y F → z ] {\displaystyle {\vec {\nabla }}\times {\vec {F}}=\det {\begin{bmatrix}\mathbf {\hat {e}} &\nabla &{\vec {F}}\end{bmatrix}}=\det {\begin{bmatrix}{\hat {e}}_{x}&{\hat {e}}_{y}&{\hat {e}}_{z}\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\{\vec {F}}_{x}&{\vec {F}}_{y}&{\vec {F}}_{z}\\\end{bmatrix}}}
Nesse caso, de certa forma, temos sim um produto vectorial entre o vector del e o campo vectorial.
Riscos do abuso de notação O uso do vector del pode gerar muita confusão – por exemplo, a multiplicação envolvendo vector del e não é comutativa, distributiva nem euclideana; também o vector del não tem magnitude nem direcção. Esses fatores podem induzir iniciantes ao erro.
Alternativas ao símbolo nabla O símbolo nabla foi introduzido por William Hamilton e rapidamente assimilado pela comunidade científica. Ainda assim, alguns autores preferem escrever a sigla de cada operador apresentado acima ao invés de usar o nabla:
∇ f = grad f {\displaystyle \nabla f={\mbox{grad}}f}
∇ u → f = u → ⋅ grad f {\displaystyle \nabla \!_{\vec {u}}\,f={\vec {u}}\cdot {\mbox{grad}}f}
∇ ∙ F → = div F → {\displaystyle \nabla \bullet {\vec {F}}={\mbox{div}}{\vec {F}}}
No caso do rotacional as siglas podem fazer referências aos termos anglófonos como "curl " ou "rotor ":
∇ × F → = curl F → = rot F → {\displaystyle \nabla \times {\vec {F}}={\mbox{curl}}{\vec {F}}={\mbox{rot}}{\vec {F}}}
Já o laplaciano pode ser representado pela letra grega delta maiúscula em vez do tradicional nabla elevado ao quadrado.
∇ 2 f = div grad f = Δ f {\displaystyle \nabla ^{2}f={\mbox{div}}{\mbox{grad}}f=\Delta f}
∇ 2 F → = Δ F → {\displaystyle \nabla ^{2}{\vec {F}}=\mathbf {\Delta {\vec {F}}} }
Notação de Einstein Na notação de Einstein substituimos a forma D J {\displaystyle D_{J}} ∂ J {\displaystyle \partial _{J}} vector del ∇ = [ ∂ J ] . {\displaystyle \mathbf {\nabla } =\left[\partial _{J}\right].}
Seja φ {\displaystyle \varphi } F = [ f J ] {\displaystyle \mathbf {F} =\left[f_{J}\right]} X = [ x J ] {\displaystyle \mathbf {X} =\left[x_{J}\right]}
grad φ = ∂ i φ ⋅ e ^ i {\displaystyle {\mbox{grad}}\,\varphi =\partial _{i}\varphi \cdot {\hat {e}}_{i}} div F = ∂ i f i {\displaystyle {\mbox{div}}\,\mathbf {F} =\partial _{i}f_{i}} curl F = | e ^ ∇ F | = ε i j k e ^ i ∂ j f k {\displaystyle {\mbox{curl}}\,\mathbf {F} ={\begin{vmatrix}\mathbf {\hat {e}} &\mathbf {\nabla } &\mathbf {F} \end{vmatrix}}=\varepsilon _{ijk}\,{\hat {e}}_{i}\partial _{j}f_{k}} Δ φ = ∂ i 2 φ {\displaystyle \Delta \varphi =\partial \,_{i}^{2}\varphi } Δ F = Δ f i ⋅ e ^ i {\displaystyle \mathbf {\Delta F} =\Delta f_{i}\cdot {\hat {e}}_{i}} A derivada direcional fica denotada por:
u ⋅ grad φ {\displaystyle \mathbf {u} \cdot {\mbox{grad}}\,\varphi }
Ver também Ligações externas «A ideia da divergência e rotacional» (em inglês) Este artigo sobre matemática é um esboço. Você pode ajudar a Wikipédia expandindo-o
 Nota: Para a tecla de computador, veja Delete.
Nota: Para a tecla de computador, veja Delete. Nota: Para Diodo emissor de luz, veja LED.
Nota: Para Diodo emissor de luz, veja LED.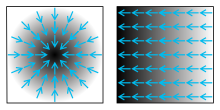




































































![{\displaystyle \mathbf {\nabla } =\left[\partial _{J}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cae7fe2d52a3e107ed745a007faa74e0d368686)

![{\displaystyle \mathbf {F} =\left[f_{J}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bff77eee2c65abcb8c8988ea19220bb2ace52a1b)
![{\displaystyle \mathbf {X} =\left[x_{J}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/273b2471b9a5ff0c0e69f77e9c259785461c51e0)


















